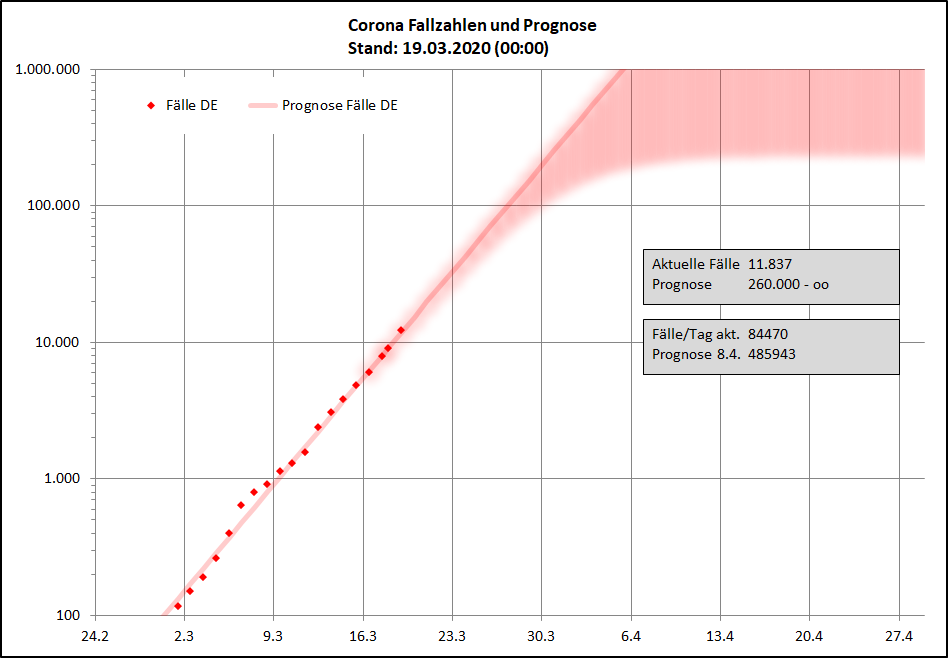
Die SARS-CoV-2 Fallzahlen folgen einer Logistischen Funktion. Dies ist unsere Modellfunktion.
Die Logistische Funktion beschreibt ganz allgemein Wachstum mit begrenzten Ressourcen.
Unter diesen Bedinungungen wachsen Populationen solange exponentiell, bis die Ressource zur Neige geht.
Das Ergebnis ist ein S-förmiger Anstieg der Population bis zu einer Obergrenze.
Die Modellfunktion wird durch Variation ihrer freien Parameter an die Daten angepasst.
Diese sog. Regression liefert genau die Form der Modellfunktion, die am besten zur Datenlage passt.
Hat man diese beste Funktion gefunden, kann man sie in die Zukunft fortschreiben und so eine Prognose stellen.
Die Logistische Funktion lässt sich durch 3 Parameter beschreiben, die im allgemeinen unbekannt sind.
Die anschauliche Bedeutung der Parameter ist:
Das Problem besteht darin, die wahrscheinlichsten Werte für die unbekannten Parameter zu finden.
Das lässt sich durch einfaches Ausprobieren und Vergleich des Funktionsverlaufs mit den Daten durchführen.
Eleganter und genauer ist eine als least-square fit (dt. Minimierung der Abstandsquadrate) bekannte Methode.
Dabei werden die unbekannten Parameter systematisch variert, bis die Summe der Abstandsquadrate zwischen realen Daten und Funktionswerten minimal wird.
Im Ergebniss findet man so gerade die Werte für t0, λ, G, die den Sachverhalt (also die Daten) am besten beschreiben.
Die Animation zeigt die Ergebnisse der Modellberechnungen ab dem 19.03.2020.
Seit einigen Tagen werden die frühen Fallzahlen nicht mehr gut durch die Modellfunktion beschrieben.
Das hat vermutlich zwei Gründe:

Das Diagramm zeigt die aktuellen Fallzahlen und die aktuelle Prognose
Die Reproduktionszahl R ist ein Maß für die Ausbreitungsgeschwindigkeit einer Epidemie. Man unterscheidet 3 Fälle:
Wenn die Epidemie ungebremst verläuft ist R während der exponentiellen Phase konstant und wird mit R0 bezeichnet.
Aufgrund der aktuellen Maßnahmen nimmt R hingegen stetig ab und ist immer nur eine Momentaufnahme.
Das RKI schätzt R in seinem
Bulletin vom 15.4 (S.14)
auf knapp unter 1.
Deutlich niedrigere Werte prognostiziert diese Analyse
der Stochastischen Fakultät, Uni Ilmenau.
Das RKI berichtet die Reproduktionszahl seit den 15.4.2020. Leider wird die Datengrundlage für die Berechnung nicht klar kommuniziert.
Ich habe daher mit dem RKI Kontakt aufgenommen um dessen Methode für eigene Berechnungen anwenden zu können.
Hier die Ergebnisse:
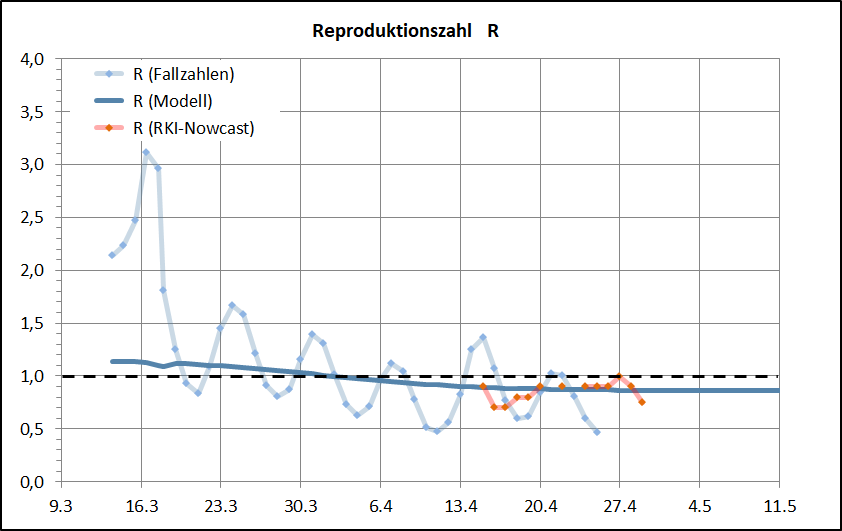
Die hellblaue Linie basiert auf dem gemeldeten Fallzahlen und weist den typischen Wochenrhythmus durch Meldeverzögerung auf.
Die dunkelkblaue Linie stellt R auf Grundlage des Prognosemodells dar.
Die rote Linie stellt die vom RKI gemeldete Reproduktionszahl dar.
Die wahre Sterblichkeit, bzw. Letalität von SARS-CoV-2, also Todesfälle/Infektionsfälle ist derzeit unbekannt, weil man die wahre Zahl der Infektionsfälle nicht kennt.
Was man kennt, ist die Fallsterblichkeit, d.h. Todesfälle/gemeldete Infektionsfälle. Über diese sprechen wir hier.
Die Fallsterblichkeit ist eine Konstante (bei konstanten Testbedingungen). Tatsächlich nehmen die veröffentlichten Werte aber stetig zu.
Dies liegt meiner Ansicht an der Vernachlässigung der Tatsache, dass Todesfälle zeitlich verzögert zu Infektionen auftreten.
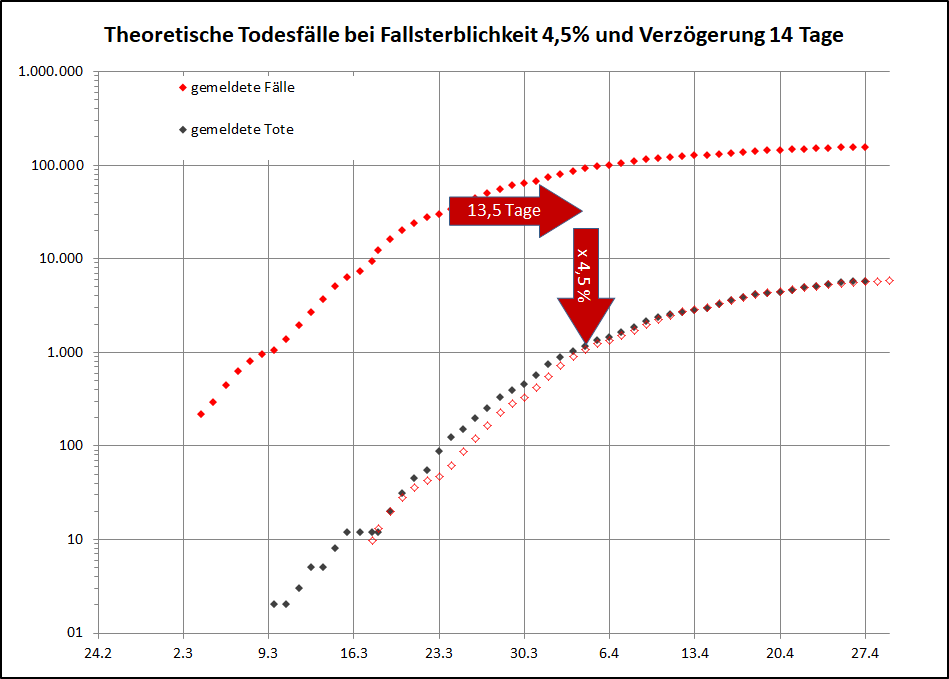
Hier der Beweis:
Die theo. Todesfälle zeigt die zeitlich verschobenen Fallzahlen mit einem konstanten Faktor multipliziert.
Das Resultat passt sehr gut zu den tatsächlich gemeldeten Todeszahlen.
Der Grundgedanke hinter den Maßnahmen gegen die ungebremste Ausbreitung des SARS-CoV-2 Virus ist,
den Verlauf zu verzögern, um das Gesundheitssystem nicht zu überlasten.
Aber über welchen Zeitraum sprechen wir, wenn wir eine Verlangsamung der Epidemie anstreben?
Nehmen wir an, dass die Epidemie ein natürliches Ende findet, wenn 10 Millionen Deutsche infiziert und immuninisiert sind.
Nehmen wir weiter an, dass wir die Ausweitung der Fallzahlen vollständig im Griff haben.
Wir können also die Maximalzahl der Fälle/Tag nach unseren Kapazitäten wählen.
Das folgende Diagramm zeigt die Entwicklung der Epidemie für:
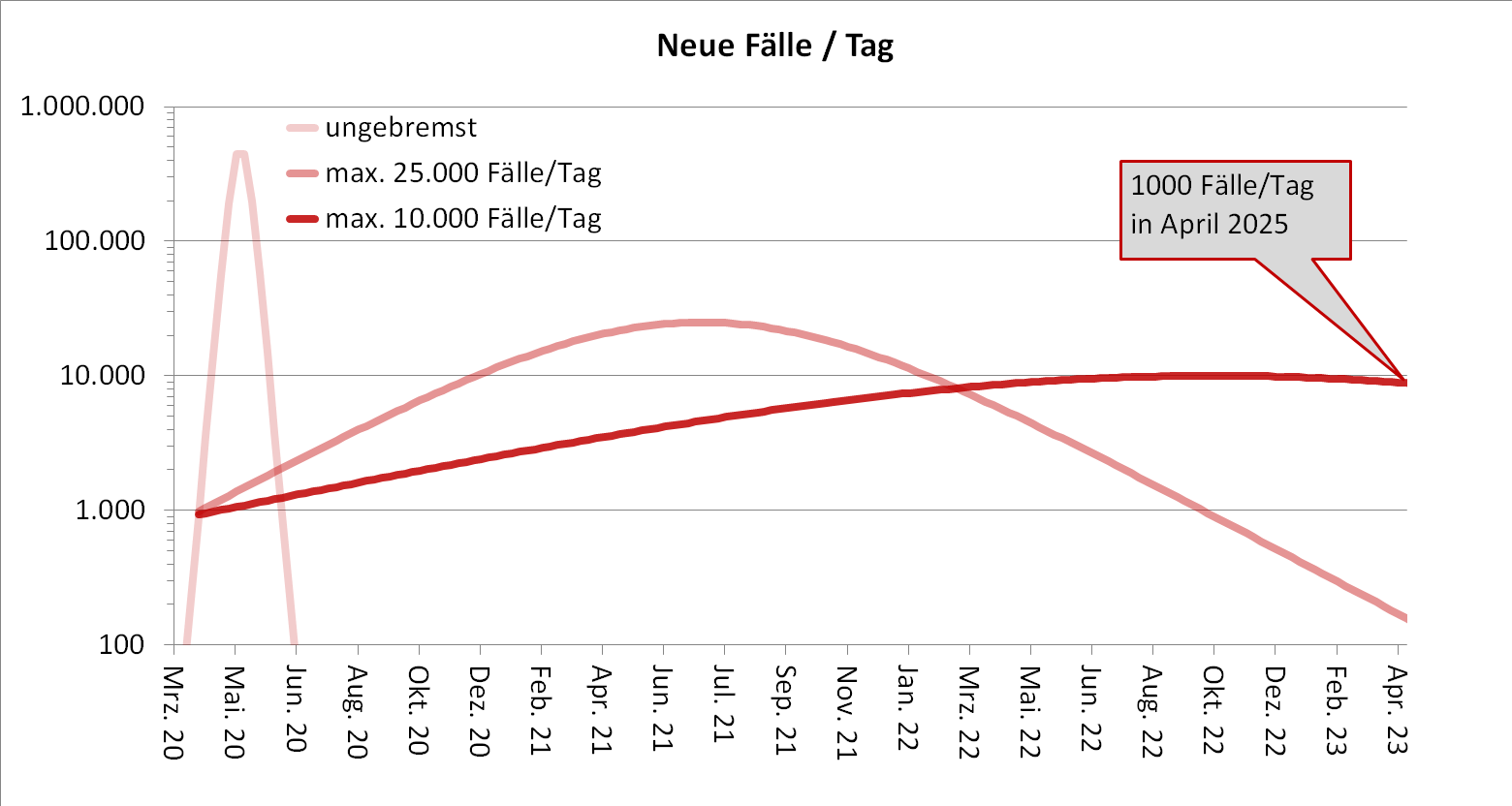
Wir haben offenbar die Wahl zwischen Pest und Cholera, bzw.
zwischen schnell und schmerzvoll und lang und mühsam.
Verantwortlich für den Inhalt dieser Seite:
Sebastian Bartel
sb(at)sciatec.de
Haftungsauschluss:
Die hier dargestelten Inhalte und Prognose sind das Ergbnbis einer mathematischen Analyse.
Sie bieten keine Gewähr, die tatsächliche Entwicklung der SARS-CoV-2 Epidemie vorauszusagen.
Daher: Achten Sie auf sich und andere und bleiben Sie gesund.
Ich bin Diplom Physiker und stelle diese Analyse ins Netz,
weil ich glaube, dass Information in dieser Zeit unser wertvollstes Gut ist.